算术逻辑单元

复习

第七章：设计完成了加法器，可以处理三个输入（两个加数和一个进位），并可以串联构成多位加法器
第八章：掌握了原码、反码和补码的概念，理解了补码可以统一加减法运算
第九章：设计完成了减法器，本质是加上一个负数（补码）
第十章：设计完成了乘法器，本质是多次加法，也可以用 Booth 算法等进行优化
第十一章：设计完成了除法器，本质是移位和减法的组合

TL;DR

算术逻辑单元（ALU）是计算机的核心运算部件
ALU 可以完成算术运算（加减乘除）和逻辑运算（与或非等）
ALU 通过控制信号选择不同的运算功能

正文

引言

　　回想一下，现在有了什么：加法，减法，乘法，除法。可以做一些基础的运算了。除此之外，还有一些逻辑操作：与，或，非，异或，移位等等。

　　注意，花十秒钟想一下，上面那些东西是怎么来的。如果不能清楚明白地了解其组成和原理，说明还没有学懂，建议回头再看一次。 这里简单提示一下：

晶体管组成逻辑门（与，或，非，异或等）；
部分逻辑门的计算逻辑与加法一致，所以组成加法器；
分出一位作为符号，在逻辑上弥补二进制减法的问题，使用模诱骗加法器在形式上做减法，形成减法器；
用加法器和减法器，组成乘法器和除法器，如果愿意，其中可以有移位器。

　　利用上面的模块，一个简单的 ALU（Arithmetic Logic Unit，算术逻辑单元）就产生了。

设计简单 ALU

　　我们可以尝试简单设计一个 4 位 ALU。

准备基本部件

　　设计的 ALU 预计有 12 个功能：加、减、乘、除、取余、与、或、非、与非、或非、异或、同或。

　　先列出需要的部件，同时列出输入和输出。

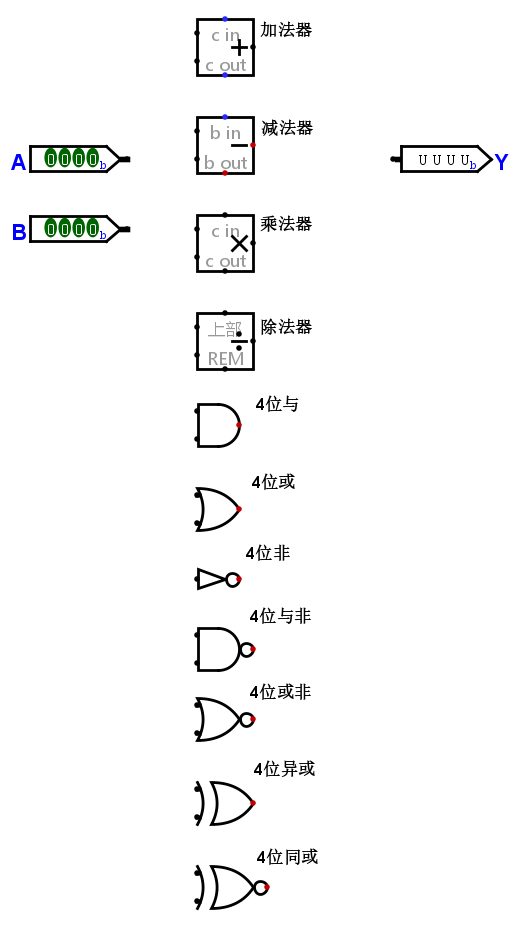
　　注意：

因为非门只有一个输入，所以此处硬编码为 A 引脚，需要取反的数值应该永远连接到 A 输入上。
加法器、减法器等等运算部件，还有一个额外的输出：溢出，所以我们也需要将它连接到输出。但因为连接这些溢出输出会使电路变得复杂，所以我们暂时不考虑连接。

连接运算电路

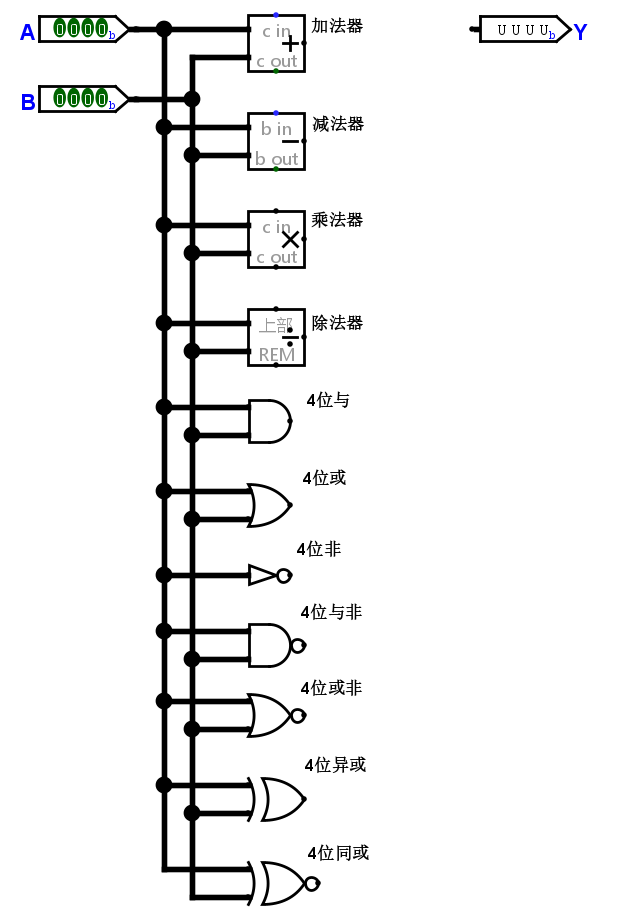
　　现在很明显问题来了。

对于这些运算的输出，连接到哪里？
所有部件都在运算，我们怎么知道哪种运算是我们需要的？换而言之，我们怎么控制 ALU 做特定的运算？

对于第一个问题

　　最简单的方法是所有运算的输出都连接到同一根输出线上，只要控制好不要数据冲突就好了，这也是最简单的方式了。

　　为此，我们需要一个控制开关：由一个控制信号 Enable 控制计算结果是否输出。

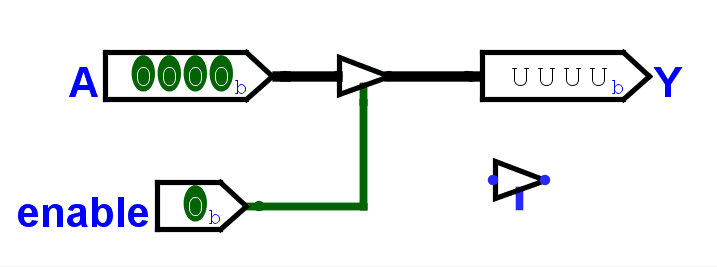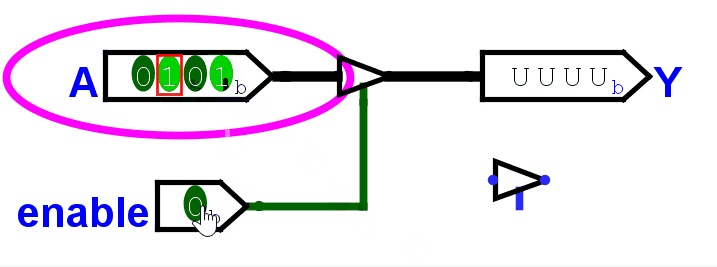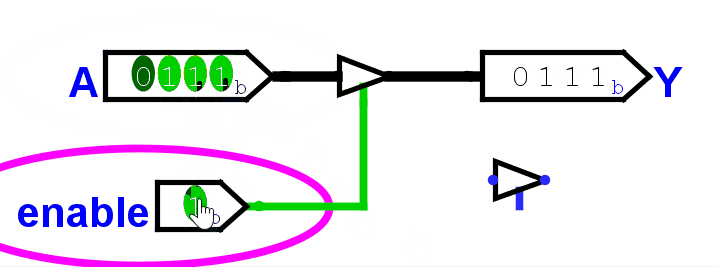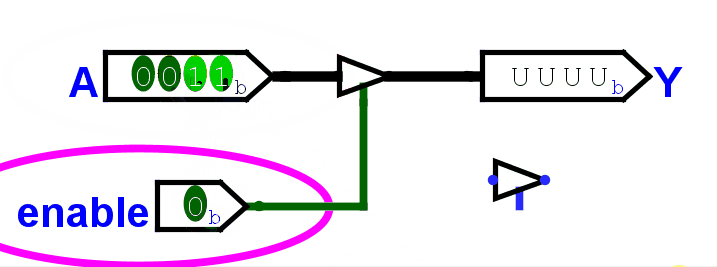
　　它的构成也很简单：

　　对于 1 位开关，真值表一画，其实就是一个与门。

输入 Data	控制信号 Enable	输出
0	0	0
0	1	0
1	0	0
1	1	1

　　对于多位开关，就是位宽个与门（4 位就是 4 个，8 位就是 8 个）。每个与门的输入都是：控制信号 + 数据信号的其中 1 位。

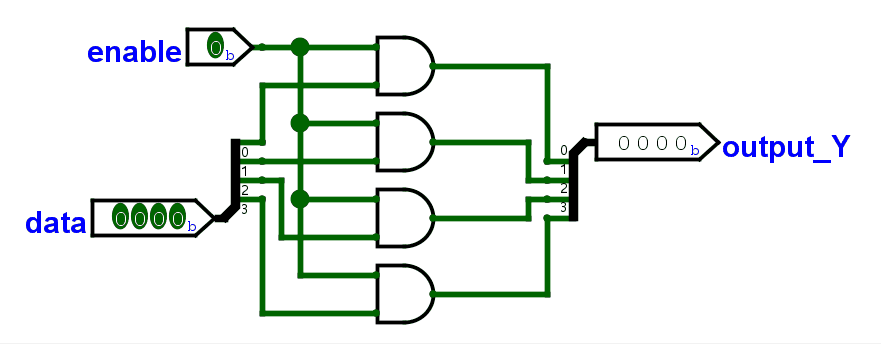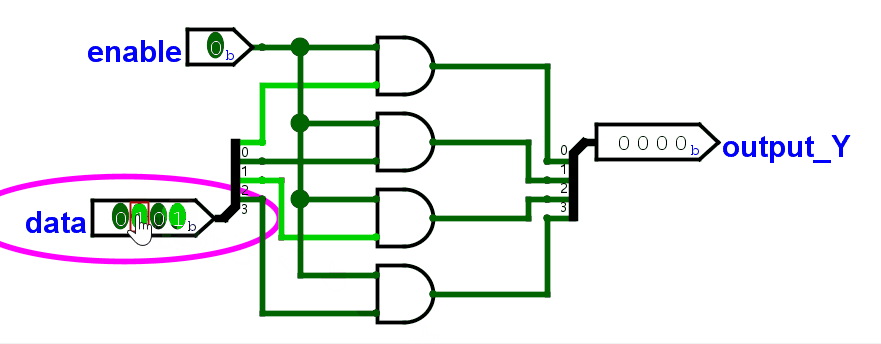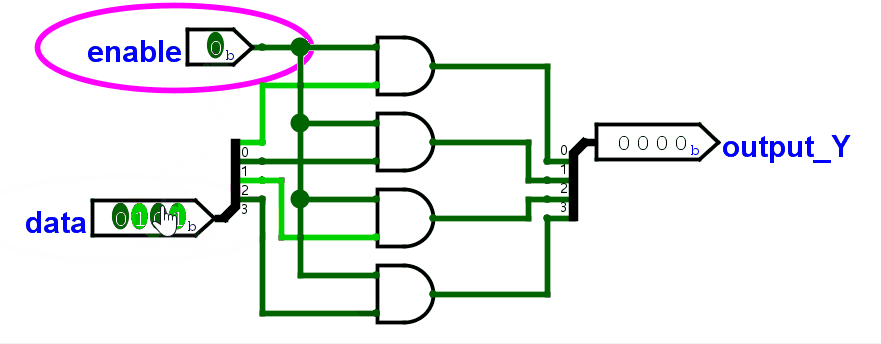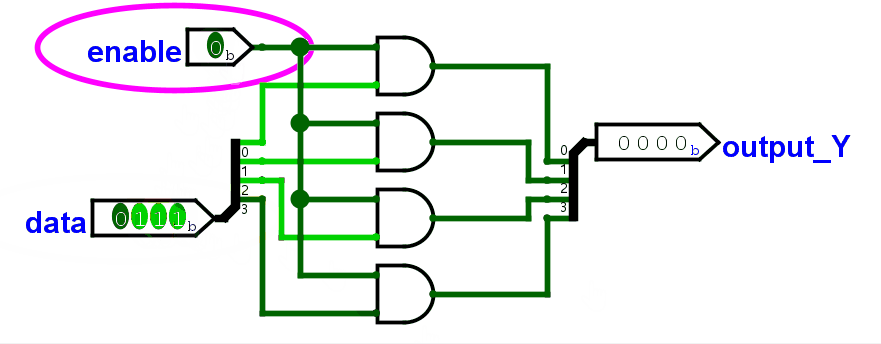
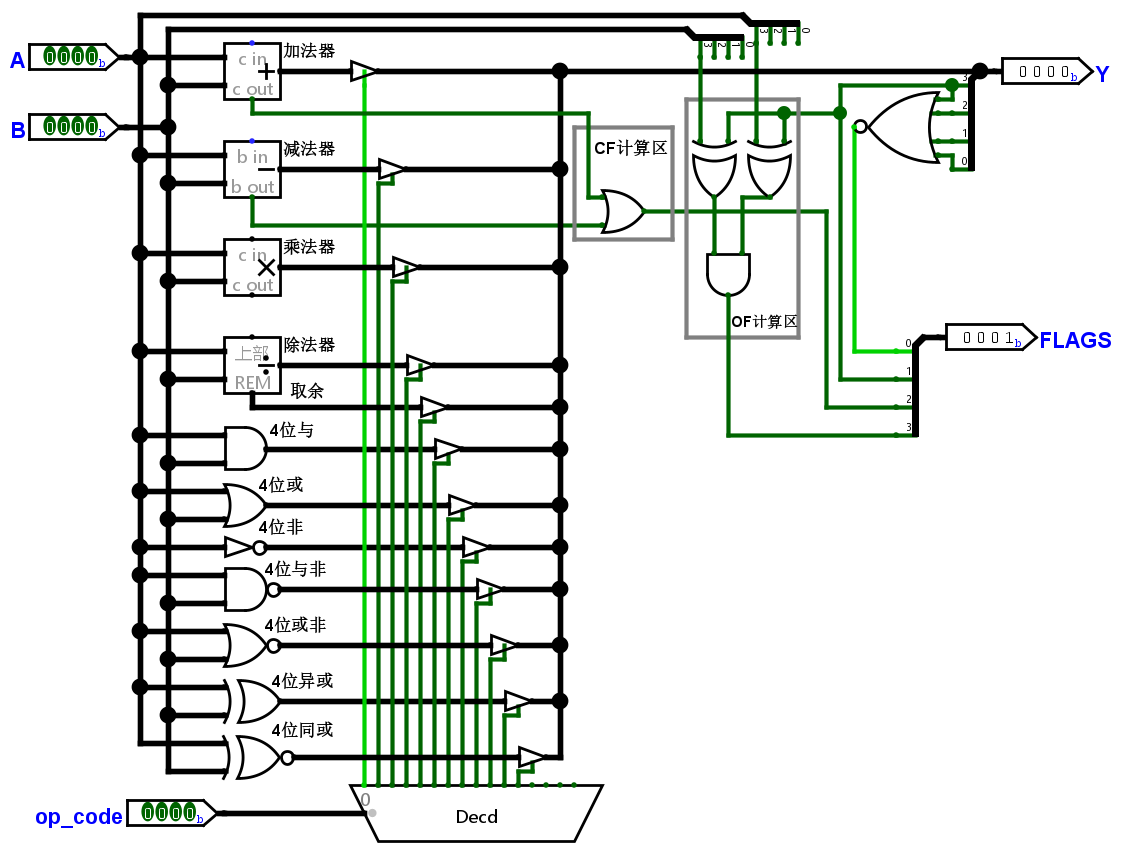
　　加上控制开关，ALU 大概是这样。

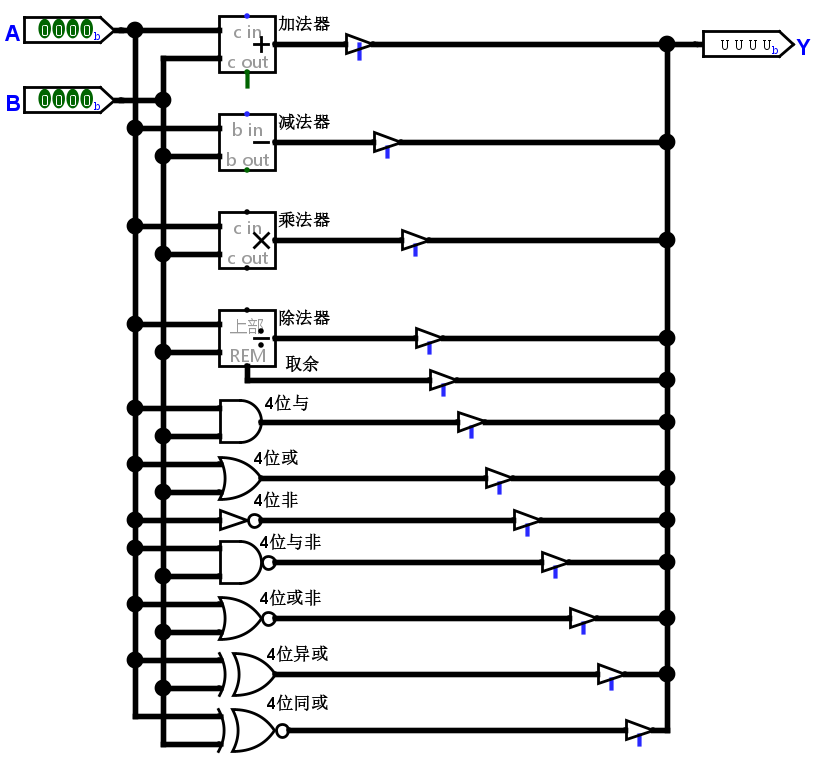
对于第二个问题

　　最简单的方法是每一种运算单独连一根线，然后根据线的通断来决定做什么运算：加法一根线，减法一根线，乘法一根线，除法一根线，等等。

　　但是！仔细考虑一下，这个简单的 ALU 就有加、减、乘、除、取余、与、或、非、与非、或非、异或、同或这 12 种运算，按照这个方法，就需要 12 根线。要是功能更强大的 ALU，运算种类更多，线的数量就会爆炸式增长，有什么办法能优化吗？

　　想一想，每一根线对应一个运算控制，而每一根线只有通电或者不通电两种状态……好像和二进制又有些像？

　　如果我们把这些线的通电状态转化为二进制数，不就可以大大压缩线的数量了吗？2¹¹ 甚至能表示 2048 种运算，但此处的 12 种运算实际上只需要 4 根线：2³(8) < 12 < 2⁴(16)。

添加选择逻辑

　　我们可以用 4 根线来表示 12 种运算。为了方便表示，我们规定：

控制信号	功能
0000	加法
0001	减法
0010	乘法
0011	除法
0100	取余
0101	与
0110	或
0111	非
1000	与非
1001	或非
1010	异或
1011	同或

　　恭喜你！我们现在已经初步接触了“指令”的概念。我们可以把上面的控制信号当作指令，告诉 ALU 做什么运算。

　　那么，我们应该怎么翻译这些指令呢？

　　有一个元件叫做译码器（Decoder），作用是把输入的二进制位翻译成特定的对象（如逻辑电平等）。看图就懂了。

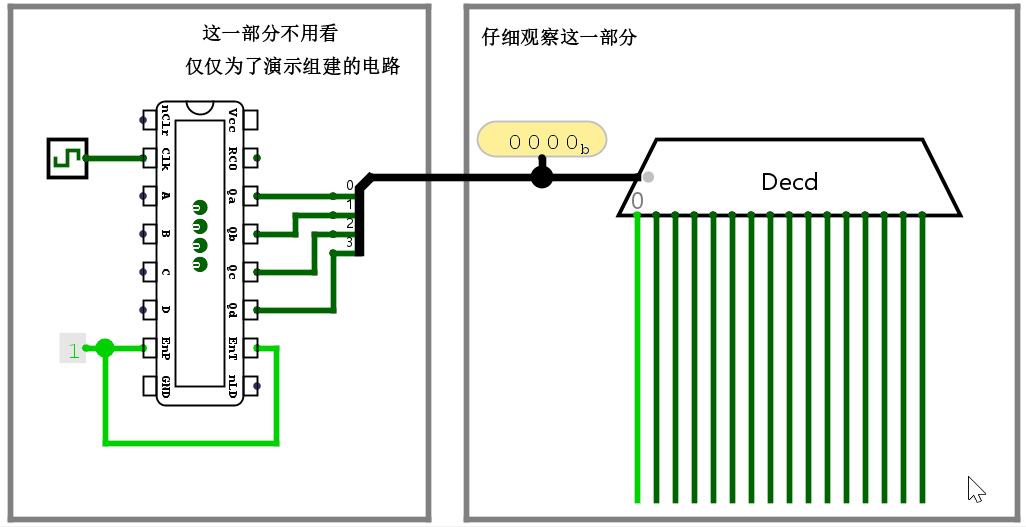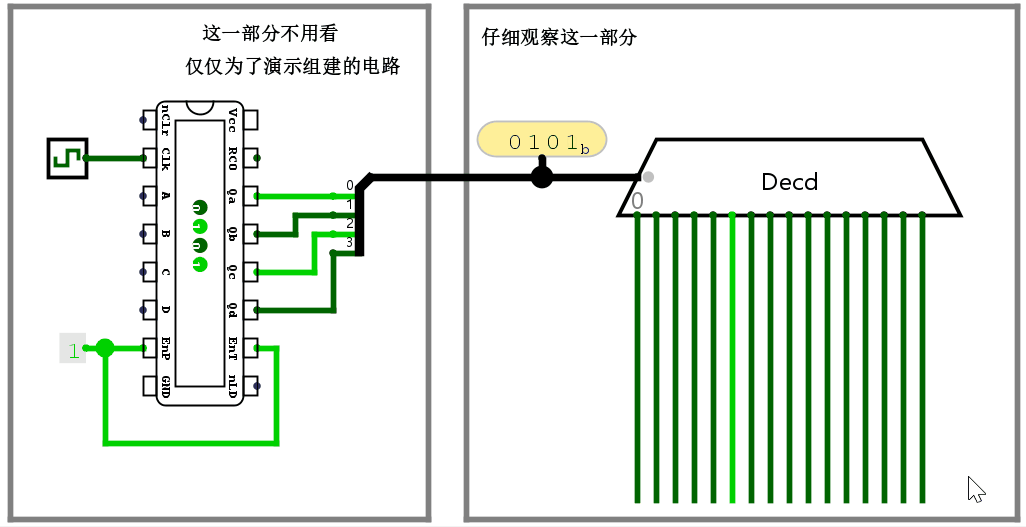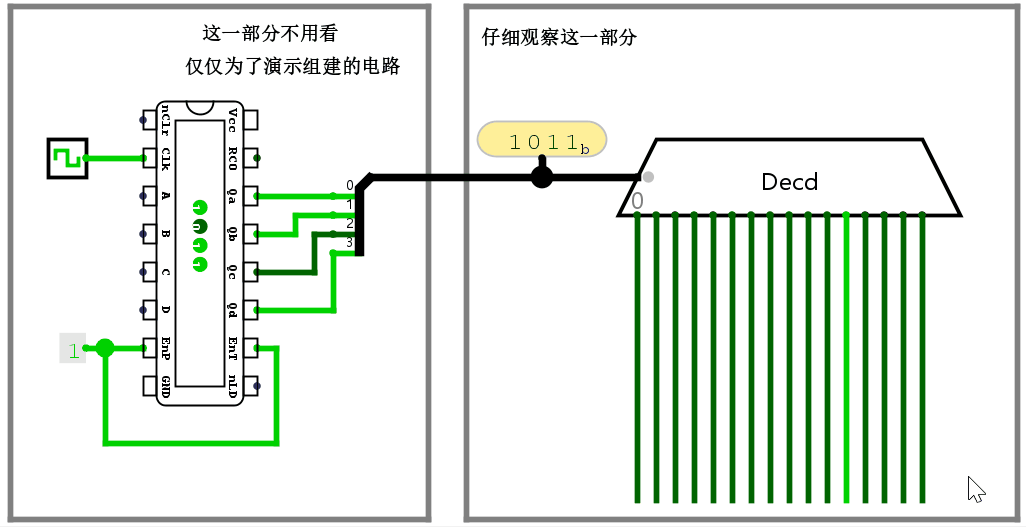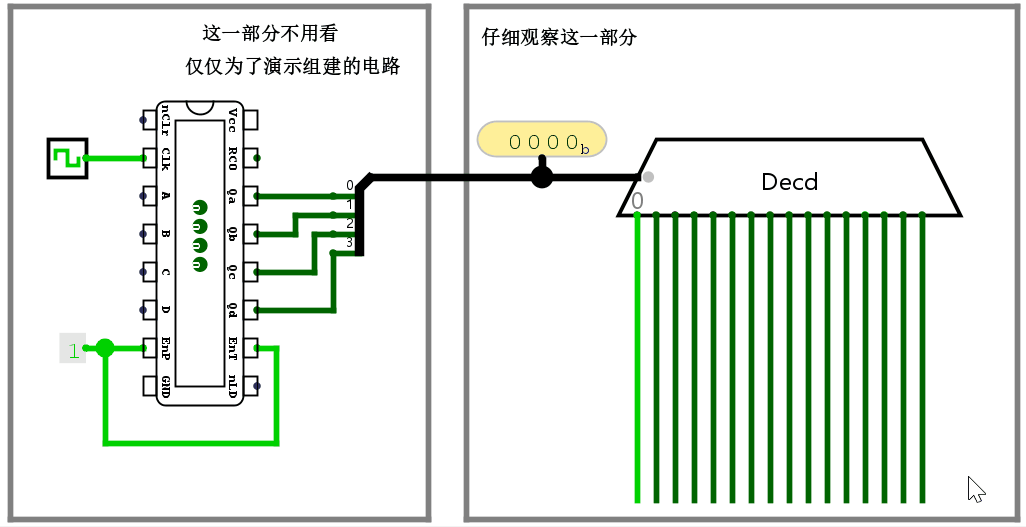
　　而上面规定的控制信号指令，恰好也递增。

　　所以我们可以额外添加一个输出 op_code（操作码），告诉 ALU 做什么运算，然后用译码器解码这个指令 op_code。

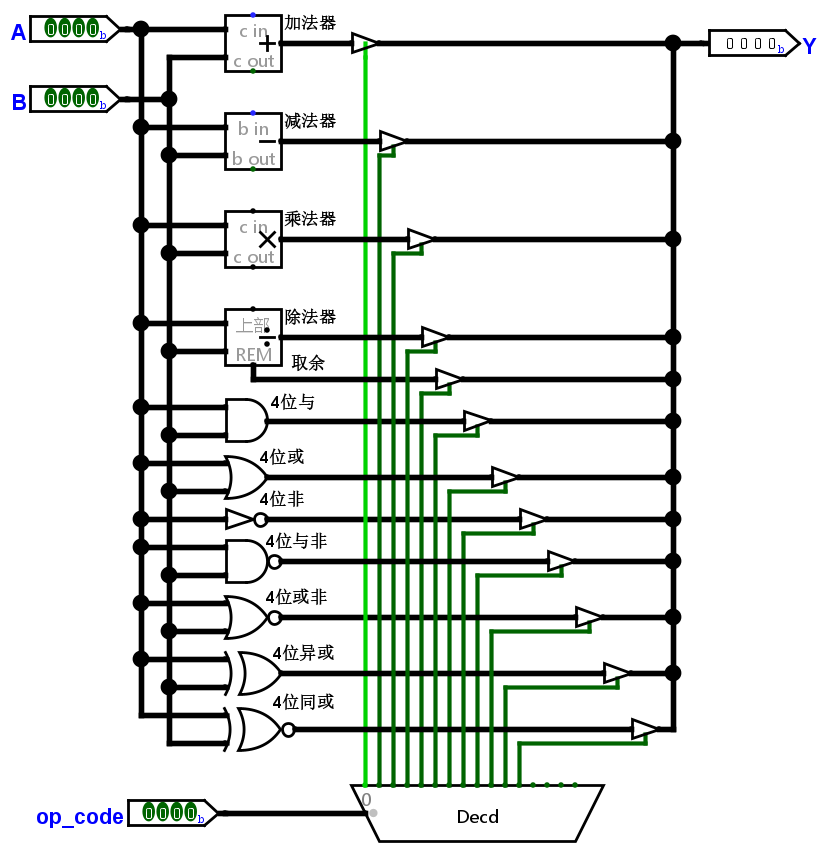
　　然后，ALU 就完成了。

验证 ALU

　　验证我们所涉及的 ALU 是否正确：设 A = 4(0100)，B = 2(0010)，根据操作码计算结果。如果正确的话，应该结果为下面这张表。

加法	减法	乘法	除法	取余	与	或	非	与非	或非	异或	同或
0110	0010	1000	0010	0000	0000	0110	1011	1111	1001	0110	1001

　　稍微把这个电路改造一下，让操作码自增，依次观察结果。

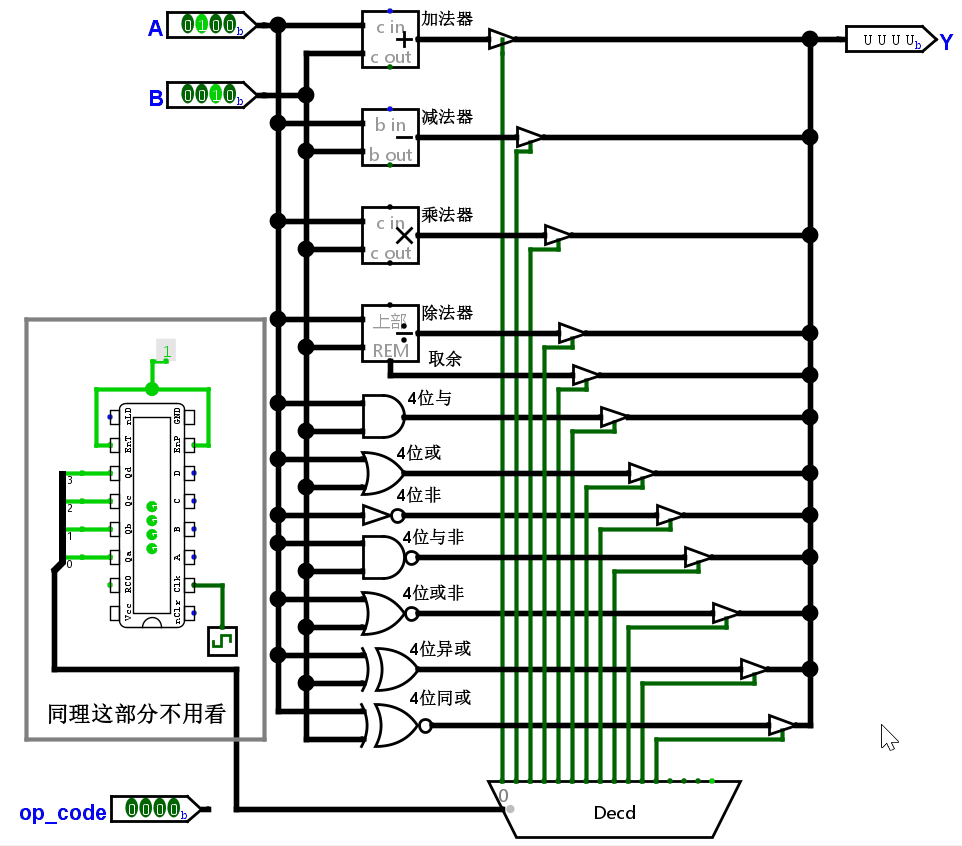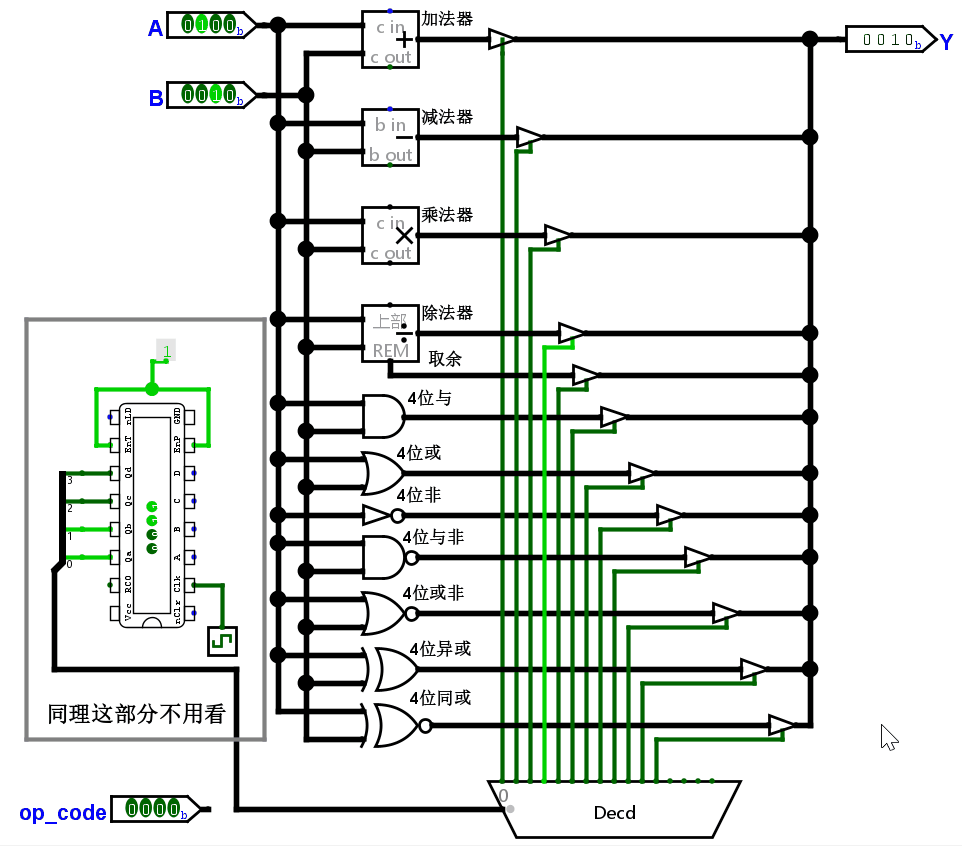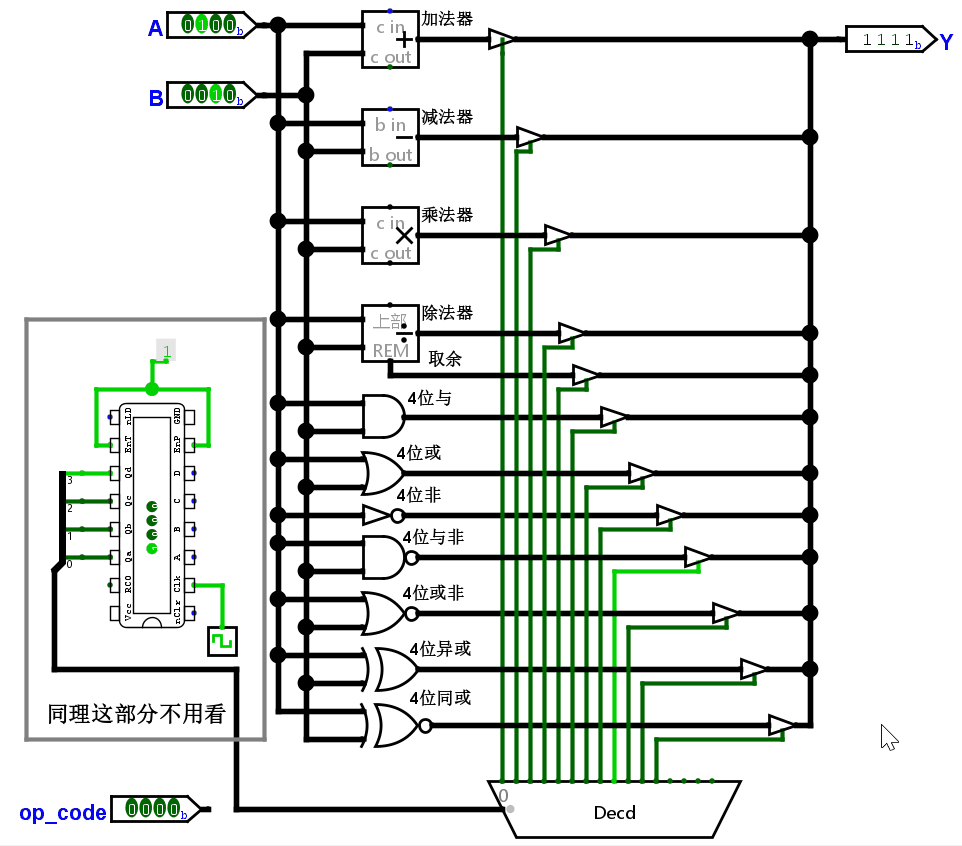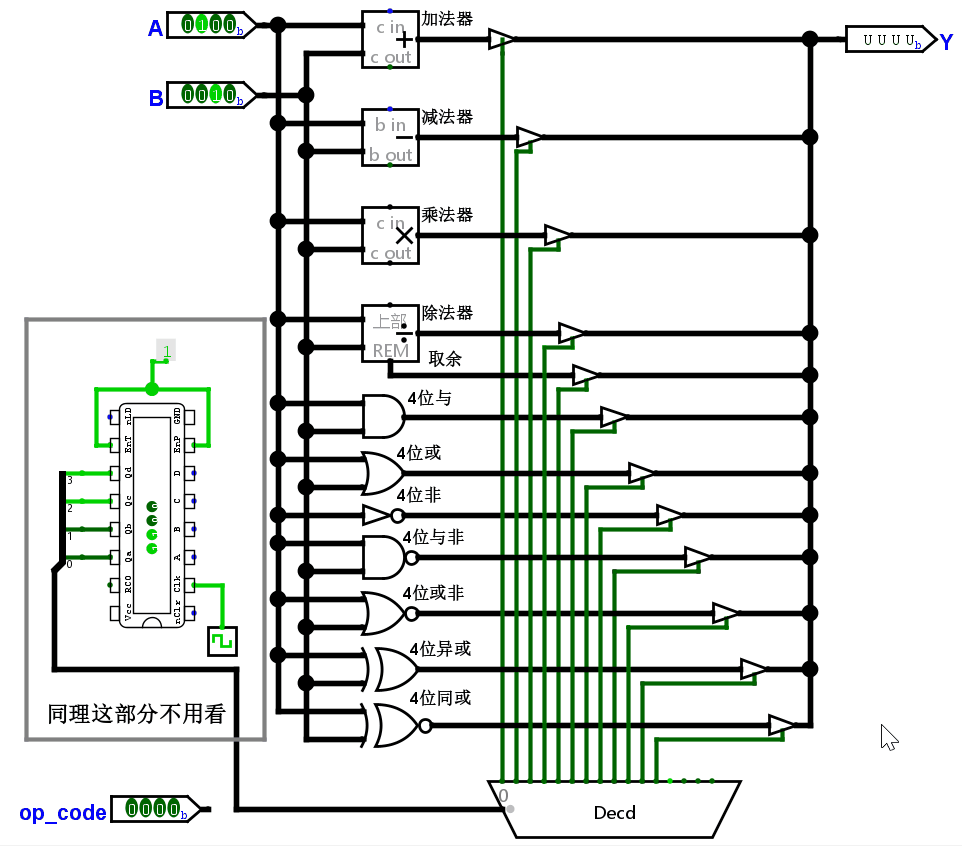
　　结果正确。

状态标志

　　现代 ALU 在运算过程中会设置一些状态标志位，用于表示运算的特殊情况：

零标志（Zero Flag，ZF）：结果为零时置 1
符号标志（Sign Flag，SF）：结果为负数时置 1
进位标志（Carry Flag，CF）：产生进位时置 1
溢出标志（Overflow Flag，OF）：结果超出表示范围时置 1

　　CF 和 OF 的区别在于，CF 对无符号数运算有意义，而 OF 对有符号数运算有意义。

4 位有符号数范围：-8 到 7，无符号数范围：0 到 15(F)
0111(7) + 0001(1) = 1000（无符号数 8，有符号数 -8）
- 执行后 CF 为 0，OF 为 1（对于无符号数，结果在范围内，没有进位；对于有符号数，结果超出范围，OF 为 1）
0111(7) + 1001(无符号 9，有符号 -7) = (1)0000（无符号数 16，因进位溢出，故输出为 0；有符号数为 0）
- 执行后 CF 为 1，OF 为 0（对于无符号数，最高位进位，CF 为 1，对于有符号数，结果没有超出范围，OF 为 0）
1000(无符号 8，有符号 -8) + 1111(无符号 15，有符号 -1) = (1)0111（无符号数 23，因进位溢出，故输出为 7；有符号数 -9，因进位溢出，输出为 7）
- 执行后 CF 为 1，OF 为 1（对于无符号数，CF 为 1；对于有符号数，结果超出范围，OF 为 1）

　　其实现代 ALU 还有其他很多状态标志位，比如奇偶标志（Parity Flag，PF）等，这里仅列出四个常用的标志位。

　　现代 ALU 还能进行比较运算，如比较两个数的大小，将在后面章节介绍。