与或非门首尾相连
复习
- 第八章:掌握了原码、反码和补码的概念,理解了补码可以统一加减法运算
- 第九章:设计完成了减法器,本质是加上一个负数(补码)
- 第十章:设计完成了乘法器,本质是多次加法,也可以用 Booth 算法等进行优化
- 第十一章:设计完成了除法器,本质是移位和减法的组合
- 第十二章:利用上面的部件,制造了一个简单的 ALU(Arithmetic Logic Unit,算术逻辑单元)
TL;DR
- 与或非门可以首尾相连
- 部分逻辑门首尾相连有一种“触发”或者“记忆”现象
正文
引言
到目前为止,我们已经了解了计算机如何进行运算:通过 ALU 执行各种算术和逻辑操作。计算机四大部件中的运算器勉勉强强算是完成了(忘记了?请返回第二章:计算机的构成,做个提醒,四大部件分别为输入设备、存储器、CPU 和输出设备)。因为 CPU 中的控制器因为有更高阶的知识,所以先暂缓。我们先将目光瞄向存储中间结果的存储器。

需要存储的理由
想象一下,如果计算机只有 ALU 而没有存储功能:
- 不能保存中间结果
- 不能记住程序状态
- 不能存储用户数据
- 每次都要重新输入数据
- 一旦输入错误就完蛋了
所以,存储功能和运算功能一样重要。
首尾相连?
之前制造的所有部件,数据都是向前流动的,为什么没有人想到将它首尾相连呢?
非门首尾相连
让我们看一个最简单的例子:一个非门的输出连接到它自己的输入。

假设初始输出为 0 -> 则输入为 0 -> 非门会将 0 变为 1,输出变为 1 -> 这个 1 又会被送回输入 -> 非门又会将 1 变为 0 -> 循环往复。
这就形成了一个振荡器,输出会在 0 和 1 之间不断交替。我们可以用这种性质,造一个时钟。后面会讲。
与门和或门首尾相连
我们再看与门和或门。
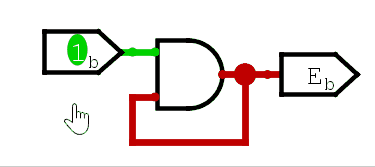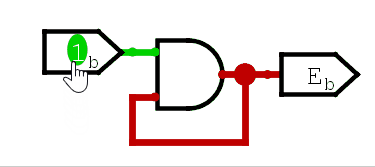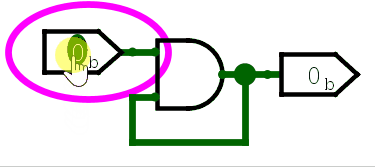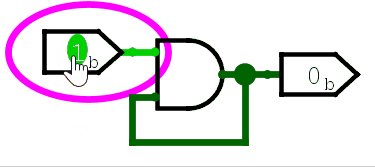
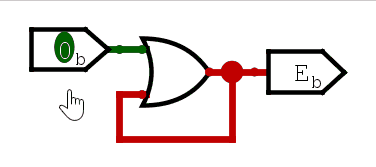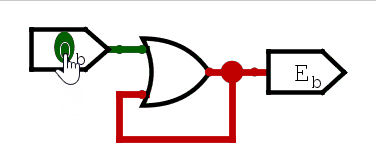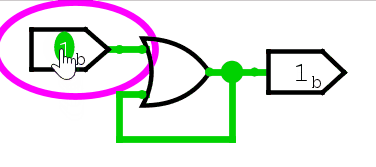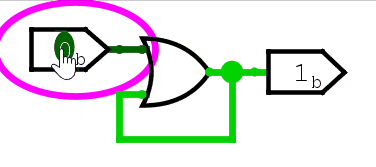
可以看到,第一次输入变化,触发了与门和或门的输出变化,但此后,无论输入怎么变化,输出都不再改变。
同样的,与非门,或非门等等,都有此性质。
这个性质,可以看成是一种简单的“记忆”——输出不再受输入变化的影响。
记忆?
如果我们能够控制这种“自己的输出又变成输入”的“反馈”现象,让电路保持在某个稳定状态,把上面的“记忆”现象改造得高端一些,会不会更好一些?
参考资料
- Wikipedia(zh):触发器:反馈电路的一个重要应用
- Wikipedia(zh):振荡器:利用反馈产生周期信号
推荐
协议
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。
封面图

设计师 | 南国微雪