第四章:负数与减法
复习
- 第一章:希望造出一台计算机。
- 第二章:这台计算机需要供能,输入,输出和处理过程。
- 第三章:利用电能和布尔代数,造出了一个加法器。
TL;DR
- 规定二进制数最高位为符号位,1 为负数,0 为正数,可以得到原码。
- 利用
相反数相加等于零可以推导出补码。 - 减去一个数,等于加上这个数的相反数,根据此定理可以诱骗加法器做减法,得到减法器。
正文
引子
加法可以计算了,减法怎么办?5 - 2 = ?
变化一下,似乎可以发现: 减去一个数,等于加上一个负数。 也即 5 - 2 = 5 + (-2),效果一样。但这个想法已经向前迈进了一大步—— 不用专门制造减法器,可以复用加法器,只需表达负数即可。
现在问题来到: 负数在计算机中该怎么表示 ?
有符号数
根据引子,现在需要表示负数。这里不得不引入有符号数的概念。
先前所有二进制表示,均默认没有符号,从 0000 表示 0 开始,到 1111 表示 15 结束,都是默认正数,然后开始一个个加,没有负数的余地。
为了解决这个问题,人们专门抽出最高位(最左位)表示符号,0 为正数,1 为负数。其余位为数值位,和原来一样。
0001表示1,1001表示-1,0111表示7,1111表示-7
需要说明的是,这里不一定需要抽出最高位,抽哪一位都可以,抽出最高位只是一种约定俗成的惯例。而且抽出最高位,在后续的电路设计中方便一点。
这种只带符号位的二进制码,叫做 原码。
原码的问题
原码有诸多问题:
- 0 占据了两个编码
0000和1000,但数学没有正负零一说; - 不能直接参与计算。
0010+1001=1011,换成十进制就是2 + (-1) = (-3),但这很明显错了;1010+0001=1011,两个加数与上面调换符号位,十进制(-2) + 1 = (-3),很明显也错了。
不能做减法,计算机就残废了。我们需要一种 能直接参与计算的 有符号数编码。
补码
没有头绪没关系,我们试着来推导。
- 首先,最简单的:
2 + (-2) = 0。应该满足相反数相加为零。 - 其次,二进制,只能用 0 或 1 表示。
- 再次,满足符号位约定:
1XXX为负数,0XXX为正数。 - 根据以上可以导出:
0010 + ? = 0000。
现在思考 ? 应该填一个怎样的二进制数。这个问题看起来没有解。右起第二位的 1 怎么可能又变回 0……
等下,似乎不是不可以—— 我们可以再加上一个 0010,然后把右起第二位进位,进位之后即为 0。 然后现在变成 0100,只是又向左推了一位。
但如果一直往左推呢?加到 4 位溢出成 5 位,然后第五位我们直接丢弃——似乎可以变成 0。
- 即:
0010 + ? = 0000 - 推出:
0010 + ? = (1)0000 - 推出:
? = (1)0000 - 0010 = 1110。 - 对于这个例子,
-210 =11102。刚好符合符号位的约定。 - 右下角的 10 和 2 表示十进制和二进制。
而对于这个推式,有一个更简单的做法: 刚好加到溢出,只需要每位取反,然后再 + 1 即可。 对于 0010 而言:0010 每位取反为 1101,然后 + 1(也即加上 0001),就可以持续进位,直到溢出。
| 符号 | 数值 |
|---|---|
0010 | |
| + | 1101 |
| = | 1111 |
| + | 0001 |
| = | (1)0000 |
所以 负数(?) = 正数(0010) 取反(1101) 加一(1110)。
通过观察发现,这个规律直到 1000 结束—— 1000 根据上述规则计算出来,负数为自身 1000,再往上 1001, 1010……计算出来的结果 0111, 0110……跟之前的正数编码相同,不能使用。
也即,从 0111 的中间 1000 为边界线,两边的数互补,相加结果为 1111。 用图表示,大概是这种感觉:

- 因为这个编码本身就是从算式(
2 + (-2) = 0)中推导出来的, 可以直接参与计算 ,叫做 补码。- 正数的补码是自身——补码本身就是从相反数的编码中推导出来的。
思考题 1
有什么便捷方法,能快速计算出补码吗?
概念
-
最高位为符号位,其他位为数值位的有符号数编码,叫做 原码 。
- 例子:
210 =00102 进制原码,-210 =10102 进制原码
- 例子:
-
原码取反 的编码,叫做 反码 。反码本质上是求补码的中间编码,而正数不需要求补,所以正数的反码是其自身。最高位也是符号位。
- 例子:
210 =00102 进制反码,-210 =11012 进制反码
- 例子:
-
原反码不能直接相加 ,例子:
510 + (-210) =01012 +11012 进制反码 = (1)00102 =210 !=310(00112)。!=为不等于- 本质上是因为有正零(
0000)和负零(1000)的存在,一个零占了两个编码。 - 原码和原码,原码和反码,反码和反码之间,均不能直接相加。
思考题 2
为什么
10002 进制补码 是-810?
减法
上述可知,减法可以表示为加上负数,而负数又用补码表示:所以将加法器的减数,变成其对应的补码即可。也即 5 - 2 = 5 + 2 的补码。
或者我们也可以说: 减法在二进制计算机里的定义是,加上 减数取反后的数值,再加一。
而补码又是取反加一,所以输入加法器之前,经过求补模块即可。求补模块 = 取反 + 加一,也可以说是减法模块。取反可以让每位都经过一次 not 门,加一可以放置一个加法器固定加上 1。
大概就像这样(图源:BiliBili 硬件茶谈):
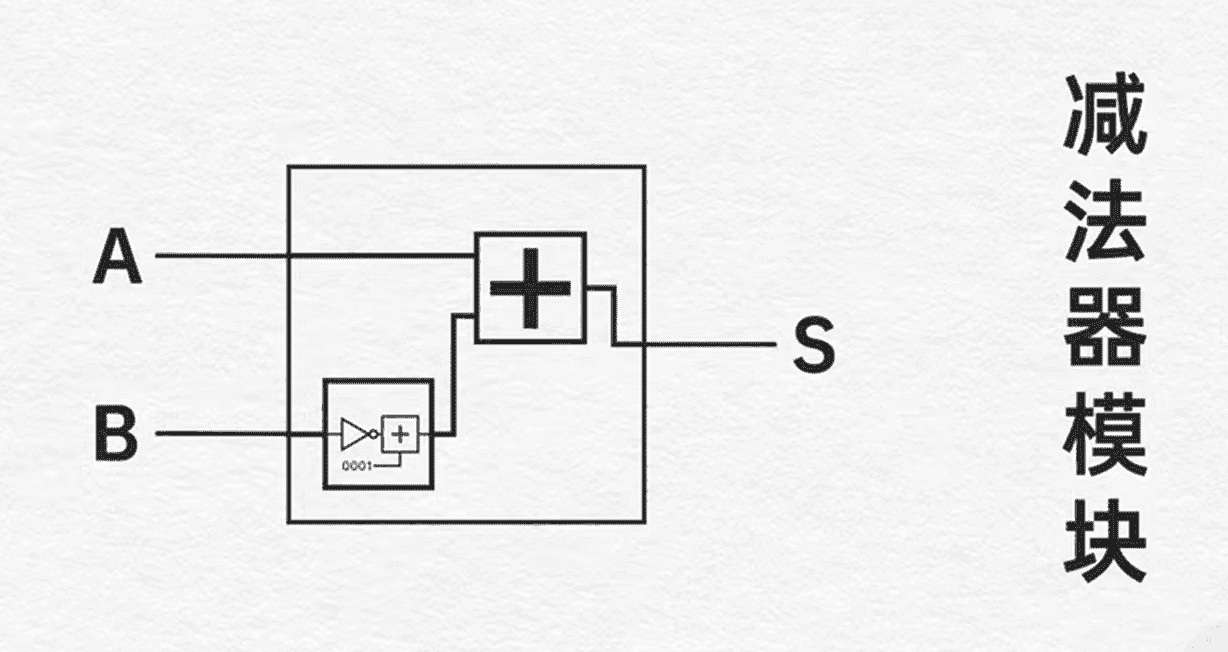
小结
知识点
- 原码
- 最高位为符号位,其余位为数值位
- 反码
- 正数反码为自身,负数按位取反
- 补码
- 反码加一
- 正数
- 原码,反码,补码,均相同
- 负数
- 原码,反码,补码,均不相同
- 减法器的构成
- 一个二进制码,现在如果要翻译成十进制,首先得问它有没有符号
参考资料
推荐
思考题答案(仅供参考)
思考题 1
一个负数的补码:写出该数相反数的二进制码,找到最右边的 1,该位及右边所有位不变,左边按位取反。
-
例子:找
-6的补码表示,先找6的二进制码(原码)——0110。然后根据上面的规律,可直接得出1010。 -
原因:
- 1 取反,为 0,再加一,最终结果仍然为 1;
- 0 取反,为 1,再加一,最终结果仍然为 0,但此过程有进位产生;
- 所以,原码 0A00 的求补过程中,若 A 为 0,低位势必会一直发生进位,直到有一个 1 处停止,所以找到最右边的 1 即可。
- 从此位截断,因为不发生进位,所以左边按位取反(只发生取反),该位及右边保持不变(发生取反和加一)
思考题 2
- 最重要的一点,如果不让
10002 进制补码 为-810,则运算会发生错误。 - 所以也人为规定了这点。
- 本质上,求负数的编码运用了数学上
模的概念。- 如时钟,
模为 12,一旦到达 12 立即回归原点,所以 12 也是 0。 - 上述加到溢出的做法,也即除模,而在 4 位有符号二进制码中,除去最高位符号位,只能表示 23=8 个数,所以
模为 8。 - 故人为规定:“正零”(
0000)为 0,“负零”(1000)为 -8。- 若规定 “负零”(
1000)为 8,则: - 0~8 会有 9 个数,而 -1~-7 只有 7 个数,严重不对称,并且运算会发生错误。
- 若规定 “负零”(
- 如时钟,
协议
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。