第五章:乘法与除法
复习
- 第一章:希望造出一台计算机。
- 第二章:这台计算机需要供能,输入,输出和处理过程。
- 第三章:利用电能和布尔代数,造出了一个加法器。
- 第四章:引入有符号数,介绍原码、反码和补码,使计算机可以表示负数和运算减法。
TL;DR
- 乘法可以看作是反复加法:预算限制高时,可以通过反复加法解决;预算充足时,可以结合 Booth 算法造出乘法模块。
- 除法可以看作是反复减法,每减一次记一次数,直到减至最后一位并溢出停止;除法也可以使用长除法,实现是位移除法,向左移位并相减。同样,具体使用哪种方法取决于成本。
正文
乘法
本质
加减法有了,乘除法呢?加法有了,逆运算的减法也就有了,只要有了乘法,而除法是乘法的逆运算,问题应该也不大。
回忆小学怎样算乘法。列竖式,相加。乘法本质是反复加法。
十进制可以这样算,二进制呢?
逐位相乘
不妨来试试: 3 × 5 = 15。 简单起见,使用无符号数,没有符号位。
0011 (3 的无符号二进制)
× 0101 (5 的无符号二进制)
--------
0011
0000# <-- # 表示占位符,没有意义
+ 0011##
--------
1111 (15 的无符号二进制)
可见竖式也能得出正确结果:0011 × 0101 = 11112 进制无符号,也即 1510。
那就好办了,让一个二进制数,与另一个二进制数的 每一位 相乘,然后进行竖式一样的 移位 操作,最后加在一起就好了。因为补码可以参与运算,所以负数的乘法也解决了,下面就是实现了。
相乘,仔细观察可以用 and(与门)解决,那—— 移位 呢?该怎么办?
Booth 算法
上述逐位相乘有一个问题:
如果是 M × 0100 这样就还好,只用加一个数字——因为只要乘数的某一位为 0,结果就必定为 0。所以逐位相乘,结果就是 0 + M + 0 + 0,实际上只用加 M 这一个数字。
如果是 M × 1111 这样的呢?就需要加四个数字——M + M + M + M。这在乘数位数变多(比如 64 位)的时候,连续的 1 将极为致命,会严重拖慢计算速度。
于是 Booth 算法优化了这一点。Booth 算法的核心思想是:对于 二进制补码 的每一位,我们可以通过判断它与它前一位的关系,来决定是否进行加减操作。
看不懂?来个实际的:设 X补码 = XsXnXn-1...X1X0, Y补码 = YsYnYn-1...Y1Y0,有 M × 00111000。
而 M × 00111000 = M × ( 23 + 24 + 25 ) = M × (01000000 - 00001000) = M × ( 26 - 23 )。
整理一下可以得出:26 × M - 23 × M,也即,在原乘数 00111000 中,10 表示连续 1 的开始,对应 - M × 23,01 表示连续 1 的结束,对应 M × 26,那么可以得出移位的规则:
| Yn+1 | Yn | 操作规则 |
|---|---|---|
| 0 | 0 | 部分积右移一位 |
| 0 | 1 | 部分积 + X补码,部分积右移一位 |
| 1 | 0 | 部分积 - X补码,部分积右移一位 |
| 1 | 1 | 部分积右移一位 |
- 为什么要右移?
- 往上划到逐位相乘的例子,计算部分积的时候,低位往往不受高位的数值影响(看上面的竖式更容易理解):
- 计算完
0011,此时部分积为0011,此后最右边的1不受后面计算的影响。 - 计算完
0011+0000#,此时部分积为0011,此后最右边的11不受后面计算的影响。 - 计算完
0011+0000#+0011##,此时部分积为1111,此后最右边的111不受后面计算的影响。 - 以此类推。
- 计算完
- 因为不受高位的影响,所以可以右移将低位挤掉,使部分积与被乘数对齐,这样可以直接计算。
- 往上划到逐位相乘的例子,计算部分积的时候,低位往往不受高位的数值影响(看上面的竖式更容易理解):
- 部分积 - X补码 怎样计算?
- 回忆一下第四章:减法在二进制计算机里的定义是,加上 减数取反后的数值,再加一
- 为什么移位规则里,
01和10的规则,一个正一个负?- 因为
10表示连续 1 的开始,对应 - M × 23,01表示连续 1 的结束,对应 M × 26 - 而上述 23 和 26,已经在移位中解决了,所以只用加减 X补码
- 因为
思考题 1
对一个数的补码再求补码,等于该数的原码吗?
移位
我们没有介绍过移位,但应该能想到,上面逐位相乘的移位,最简单的方式,就是在最后一位后面补零,同时丢掉最高位(以上述竖式的中间结果为例):0011 不补零,0000 补一个,0011 补两个。
而在对有符号数进行移位时,特别是右移,最高位需要补上符号位 。也就是说:对 1010 进行右移,结果应该为 1101。
思考题 2
我们现在只有加法器,应该怎样移位和补位?以及, 设计一个最简单的乘法器,真的需要移位吗?
除法
本质
除法是乘法的逆运算,本质是反复减法。
例如,我们要计算 12 ÷ 3,可以看作是不断从 12 中减去 3 直到不能再减为止:
12 - 3 = 9
9 - 3 = 6
6 - 3 = 3
3 - 3 = 0
因此,得到结果 4,也即减去的次数。
此实现需要进行多次减法运算,效率低下。为了提高运算效率,我们需要更高效的算法。
长除法
长除法是我们平常手算除法的方式:先将被除数的高位和除数对齐,然后用除数去除被除数,得到商和余数,再将余数和下一位对齐,继续除,直到被除数的所有位都处理完毕或者余数为 0。以 1011012 ÷ 1012 为例:
1001
_______
101)101101
101
_______
101
101
_______
0
短除法的复杂程度与位数成正比。除数位数越大,长除法效率越低。
计算机底层可以实现更高效的除法算法(牛顿迭代法、二分法等),但是否实现取决于成本,高效除法比较复杂,此处略去不讲。
长除法通常使用移位和减法来实现,也被称为 位移除法 (向左移位再相减)。
小结
知识点
- 乘法
- 本质
- 逐位相乘
- Booth 算法(对逐位相乘的优化)
- 除法
- 本质
- 长除法
参考资料
- Wikipedia(zh):Booth 算法
- Wikipedia(zh):长除法
- Wikipedia(zh):位操作#移位
- BiliBili:计算机怎样计算乘法
- Booth 算法过程具体示例
- Booth 算法过程抽象总结
推荐
思考题答案(仅供参考)
思考题 1
回想一下,补码究竟是怎样推导出来的——相反数相加为零。所以,对一个数的补码再求补码,其实就是对一个数的相反数再求相反数,其结果必然等于自身。
二进制中,特殊在于:
- 减法的定义为:加上 该数取反后的数值,再加一
- 负数的定义为:该数取反后的数值,再加一
这两种说法本质上是相同的:- X,可以是 X 的负数,也可以是 0 减去 X。 有趣的地方在于:
- 如果我们将 X 按照定义进行两次求补,也即
~(~X + 1) + 1,它并不等于X + ~1 + 1
思考题 2
- 移位可以使用 or 和 xor 门,也可以将输入直接与输出错位相连。错位直接相连肯定比使用逻辑门效率更高,速度更快(图源:Wikipedia)。
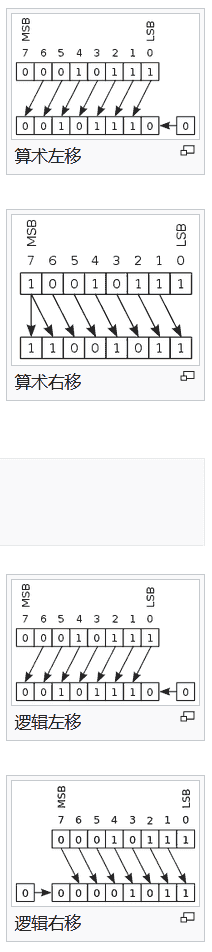
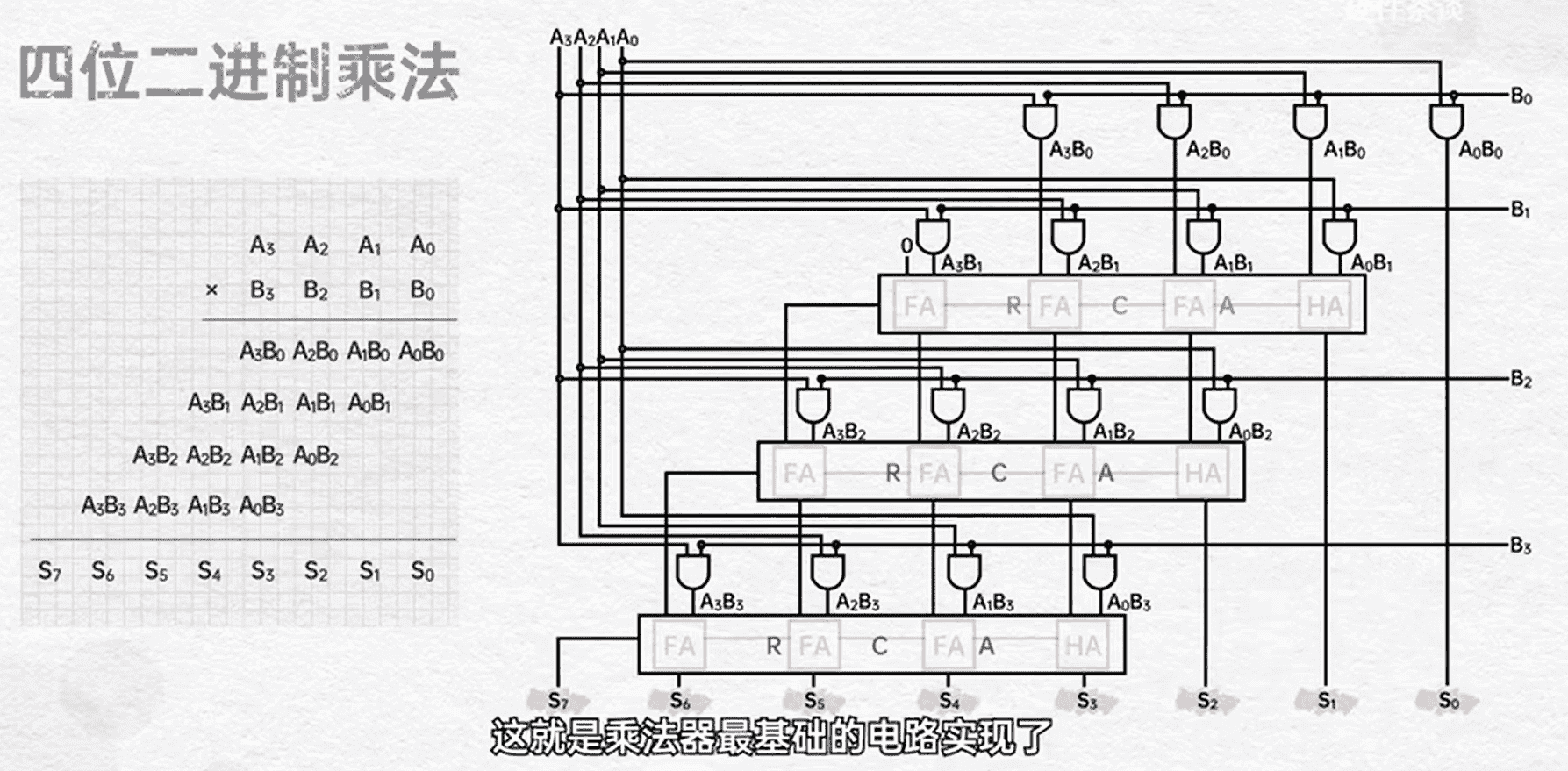
- 其实最简单的乘法器不需要移位,只需要错位相加,当中错位可以让低位直接输出(图源:BiliBili 硬件茶谈)。
协议
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。