第七章:存储器
复习
- 第二章:这台计算机需要供能,输入,输出和处理过程。
- 第三章:利用电能和布尔代数,造出了一个加法器。
- 第四章:引入有符号数,介绍原码、反码和补码,使计算机可以表示负数和运算减法。
- 第五章:介绍乘法与除法,并尝试从原理上优化效率过慢的问题。
- 第六章:组成算术逻辑单元,负责计算,模块化。
正文
引子
计算功能设计完成,但是哪怕一次微小扰动,都会使最终的结果立即变化。所以,为了保存中间结果,接下来需要一个东西,将其存起来。
锁存器
首尾相连
回想一下,非门将输入取反。那如果首尾相接会怎么样?非门会直接短路吗?
正如上面的图所示,非门不仅不会短路,而且输出会一直在 0 和 1 之间跳动。这是一个非常有意思的事情。 利用这个性质可以做一个简单的时钟。
时钟 就是字面意思,就像一个钟表一刻一刻地走, 用来标记时序 ,但现实时钟有 12 个单位,会从 1 走到 12 然后归位,而二进制时钟只有 2 个单位,所以 时钟会一直在 0 和 1 中间跳变,永不停息 。
之所以是简单的时钟,是因为当逻辑门叠加越多,其延迟越高。 而非门首尾相连构成的时钟跳变速度极快,其他逻辑部件(如加法器、乘法器、锁存器、触发器和选择器等)变化跟不上。简单起见,我们假设所有部件跳变速度一致,不存在这个问题。
那与门和或门各自首尾相连,会有什么效果呢?
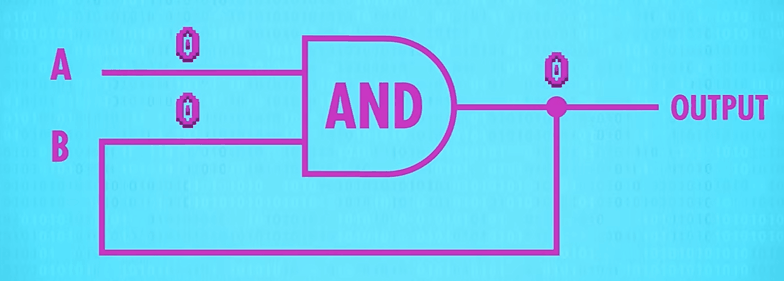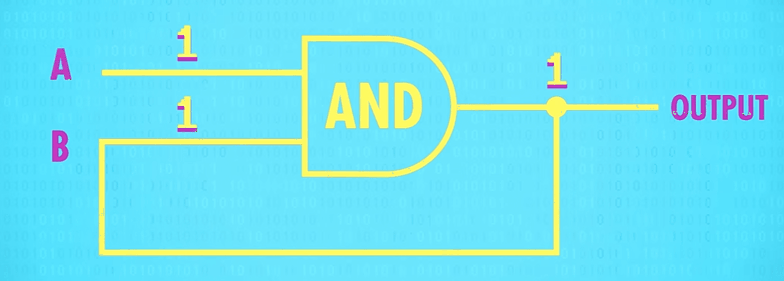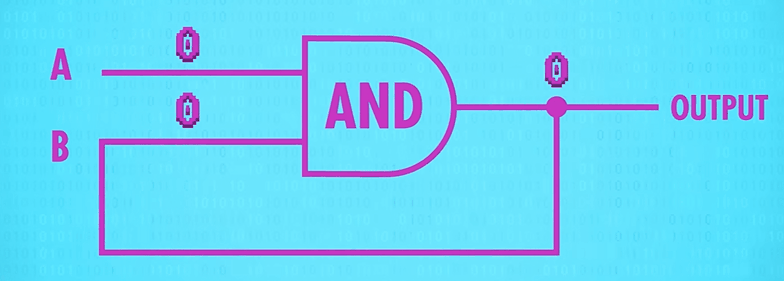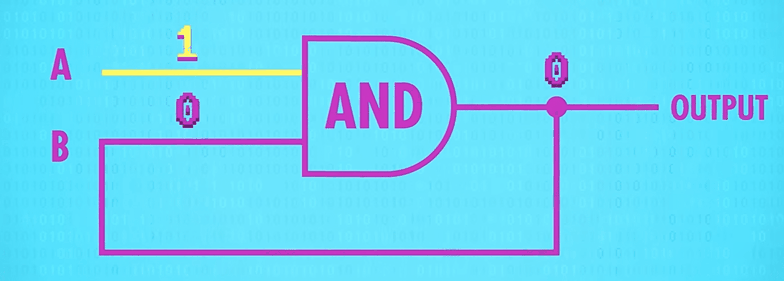

与门和或门在某次输入一个信号之后,无论怎样改变输入值,都不会再改变输出值了。也就是说,有个信号“触发”了变化。
这给了我们一个很重要的启示: 逻辑门可以首尾相连,达到意想不到的效果。
AND-OR 锁存器
接下来我们把三大逻辑门按照下面的顺序,连接起来,形成一个奇怪的结构,研究它的真值表。
- 结构
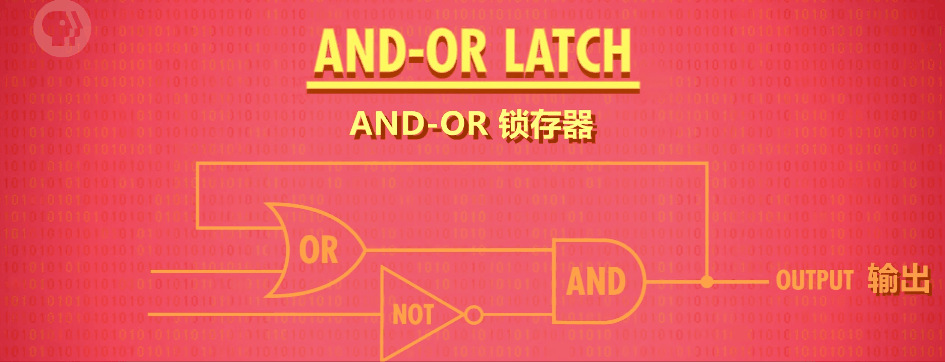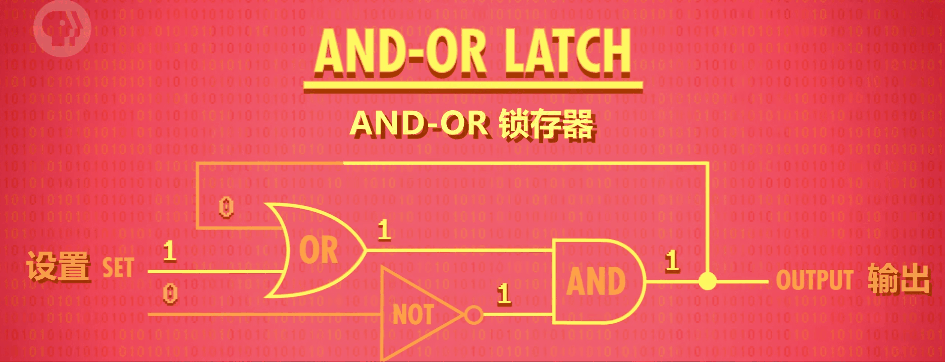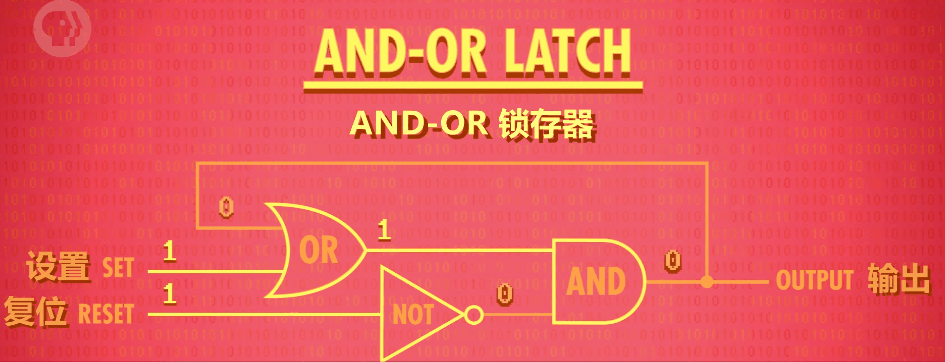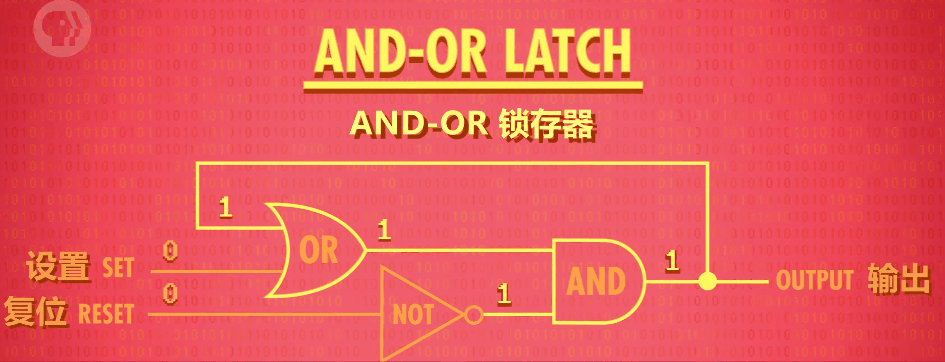
- 真值表
| 设置端 S(et) | 重置端 R(eset) | 输出 Y |
|---|---|---|
| 0 | 0 | 上一次的输出 Y |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
当 S = 0 并且 R = 0 时,下一次的输出 Y 取决于图中或门的另一个引脚,而该引脚连接到了上一次的输出 Y。所以,下一次的输出 Y 等于上一次的输出 Y。 换句话说,当 S = 0 并且 R = 0 时,这个结构锁住了输入的值。
- 如果觉得不好理解,把三种情况列出来就明白了:
- 当 S = 1 , R = 0 变为 S = 0, R = 0 时,之前的输出 Y 为 1,变化后为 1,之后也一直为 1
- 当 S = 0, R = 1 变为 S = 0, R = 0 时,之前的输出 Y 为 0,变化后为 0,之后也一直为 0
- 当 S = 1 , R = 1 变为 S = 0, R = 0 时,之前的输出 Y 为 0,变化后为 0,之后也一直为 0
所以,这个结构,具有记忆和存储的功能。取名为:AND-OR 锁存器。
D 锁存器
上面的设计虽然达到了目的,但还是有些复杂,所以,我们打算只用两个输入端:D(Data) 为数据端,WE(Write Enable,允许写入) 为控制端。
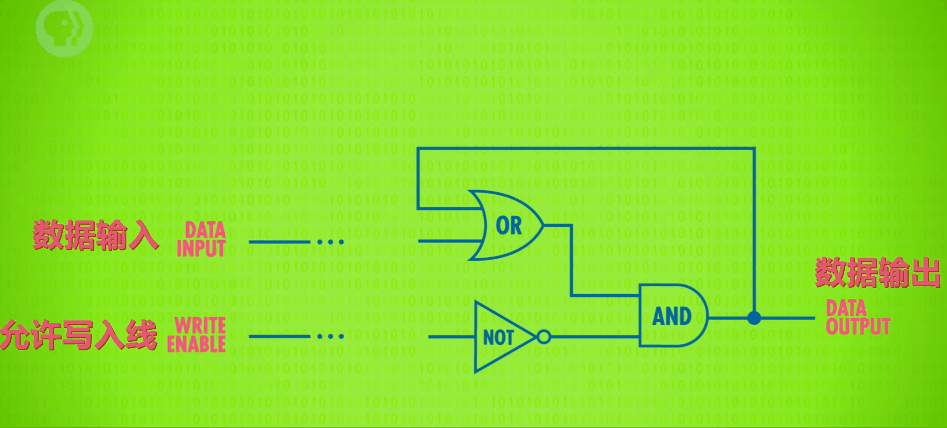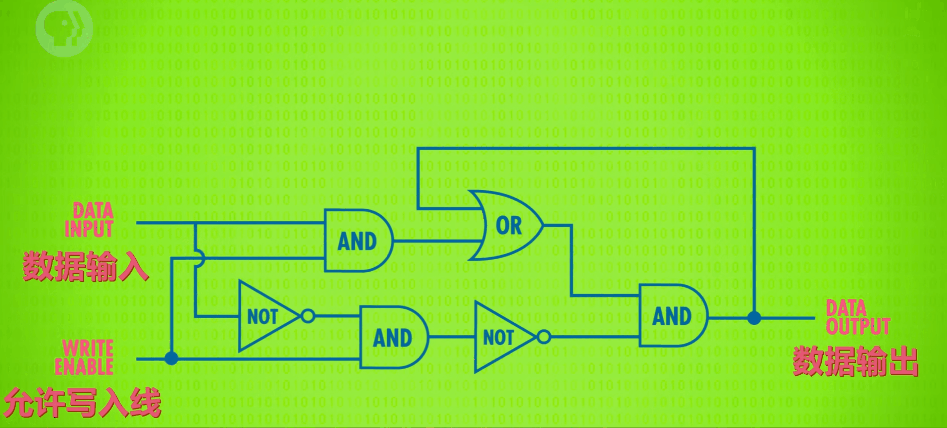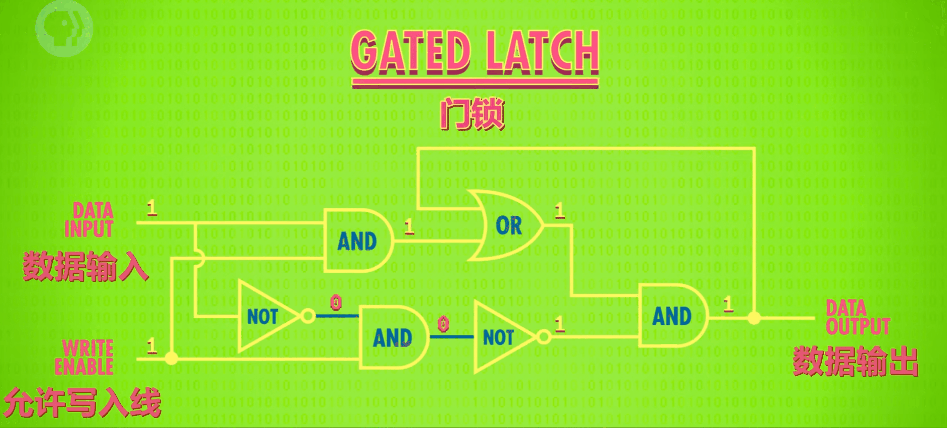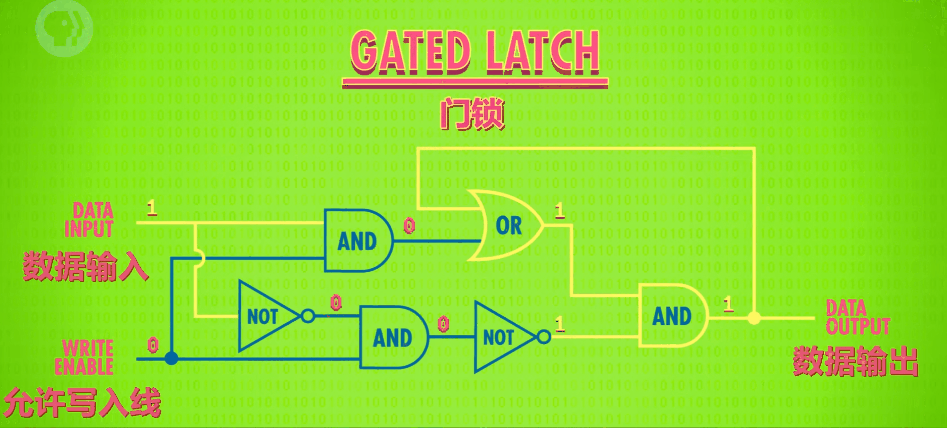
功能为: 当 WE 为 1 时,输出 Y 的值等于输入端 D 的值;当 WE 为 0 时,不允许写入,输出 Y 的值为上一次输出的值。
触发器
SR 触发器
上述 AND-OR 锁存器可以采取另一种逻辑门实现方案,如下所示:
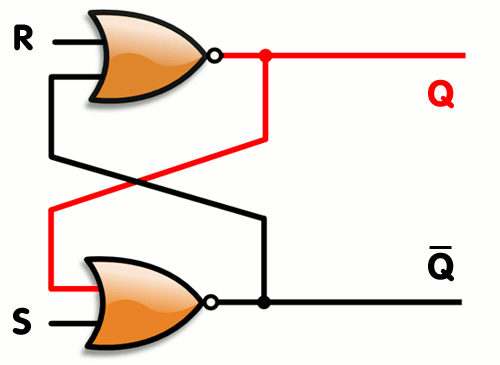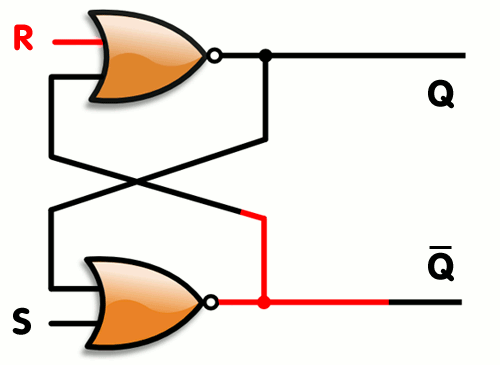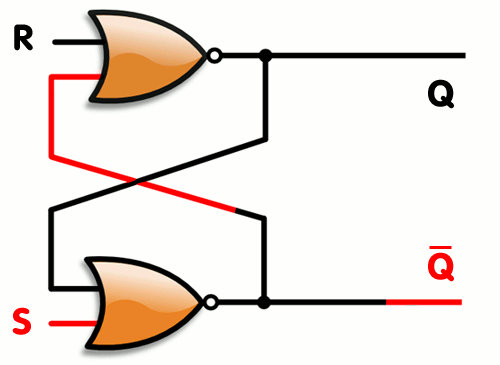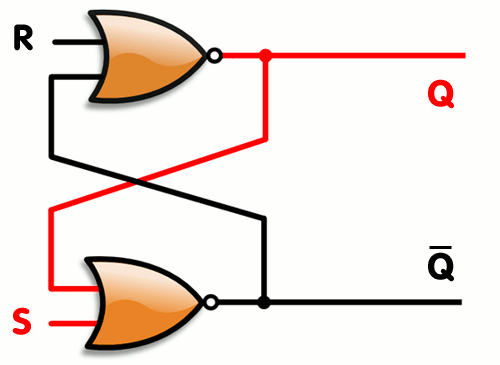
注意,图中是 nand,也即与非门,从晶体管的角度来说,nand 门要更划算(详见第三章:简单逻辑门的补充部分)。
这个东西有另一个名字:SR 触发器。SR 触发器有两个输入端:S(Set) 为设置端,R(Reset) 为重置端。
- 特征方程(输出公式):Qnext = S + R · Q,且 R · S = 0
- R
- 意为 R 的反相,即 R 取反后的值,读作:R 反
- 部分教程写作
R',写法不同,效果相同
- R · S
- 意为 R 与 S,也意为 R 和 S 取 交集
- 离散数学和集合论术语,等同于 R ∧ S
- 在二进制运算上可以 一定程度上 等同于 乘法 运算
- R + S
- 同理, 意为 R 或 S,也意为 R 和 S 取 并集
- 离散数学和集合论术语,等同于 R ∨ S
- 在二进制运算上可以 一定程度上 等同于 加法 运算
- 运算优先级,同十进制加法和乘法运算法则:先乘后加,括号先算
- 后文真值表中 X 为 无意义 或者 任意值均可
- R
- 状态转移表
| S | R | Qnext | 动作 |
|---|---|---|---|
| 0 | 0 | Q | 保持 |
| 0 | 1 | 0 | 重置 |
| 1 | 0 | 1 | 设置 |
| 1 | 1 | X | 不允许的输入 |
- 激励表(专业术语,意为上一个输出怎样 影响或激励 下一个输出,所以 Q 在前)
| Q | Qnext | S | R |
|---|---|---|---|
| 0 | 0 | X | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | X | 0 |
电平触发和边沿触发
感觉一切都很完美了。 但是如果输入的信号并不是期望的信号,而是被干扰的信号呢? 比如,希望输入 1,但在传输过程中,由于发热或者噪声等原因,导致电子能量逐渐减弱,降到门电压阈值之下,被逻辑门看作了 0。那么输出不就全错了?
为此,计算机科学家们设计了根据时钟跳变变化的的边沿触发。边沿是指 1 跳变为 0 或 0 跳变为 1 的一瞬间。根据跳变的方向不同,可以分为上升沿和下降沿,因此触发器也分为上升沿触发和下降沿触发。
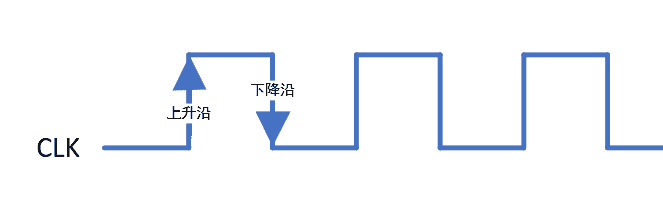
边沿触发可以有效解决传输错误的问题。电平只有在单方向跳变时才发生改变,所以电平被干扰和电平反方向跳变均不会引起改变。
D 触发器
改造上述的 D 锁存器,改为边沿触发。同样,两个输入端:D(Data) 为数据端,但 WE(Write Enable,允许写入) 改为 Clk(Clock,时钟脉冲) 作为信号端,接受一个上升沿或下降沿作为有效输入,其他时间无论高电平和低电平,均视为不允许写入。
D 触发器的功能是: 当每一个上升沿或下降沿触发 Clk 端时,将 D 端目前的值输出并锁存。
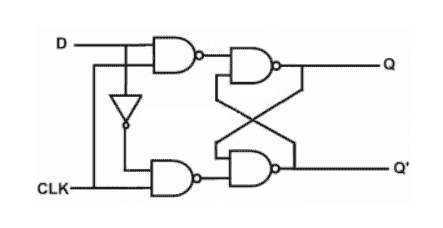
- 特征方程(输出公式):Qnext = D
- 真值表
| D | Clk | Q | Qnext |
|---|---|---|---|
| 0 | ↑(上升沿) | X | 0 |
| 1 | ↑(上升沿) | X | 1 |
| X | 0 或 1 | 0 | 0 |
| X | 0 或 1 | 1 | 1 |
JK 触发器
JK 触发器过于复杂,此处不展开。只贴出其原理图、真值表和输出公式,感兴趣的读者可以自行推导。
- 原理图
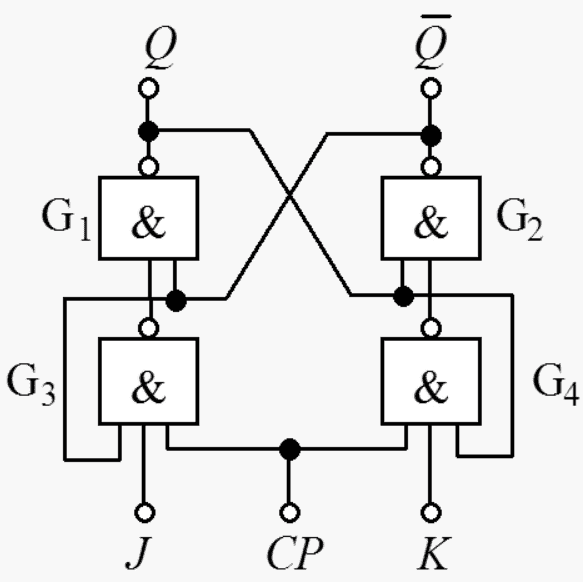
- 特征方程(输出公式):Qnext = K · Q + J · Q
- 状态转移表
| J | K | Clk | 动作 | Qnext |
|---|---|---|---|---|
| 0 | 0 | ↑ | 保持 | Q |
| 0 | 1 | ↑ | 重置 | 0 |
| 1 | 0 | ↑ | 设置 | 1 |
| 1 | 1 | ↑ | 反转 | Q |
| X | X | 0 或 1 | 保持 | Q |
- 激励表
| Q | Qnext | 动作 | J | K |
|---|---|---|---|---|
| 0 | 0 | 不变 | 0 | X |
| 0 | 1 | 设置 | 1 | X |
| 1 | 0 | 重置 | X | 1 |
| 1 | 1 | 不变 | X | 0 |
存储器
将上面的锁存器或触发器连接起来,可以形成存储器。
简单排列
简单堆叠 8 个、16 个、32 个、64 个锁存器或触发器,可形成 8 位、16 位、32 位、64 位的存储器。
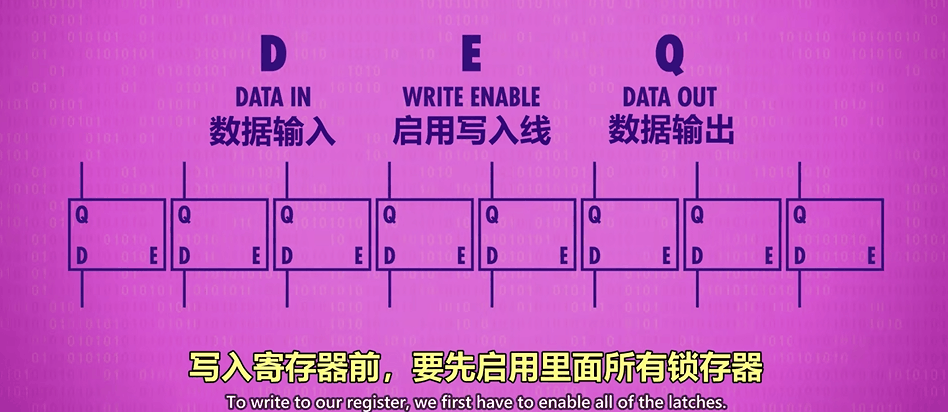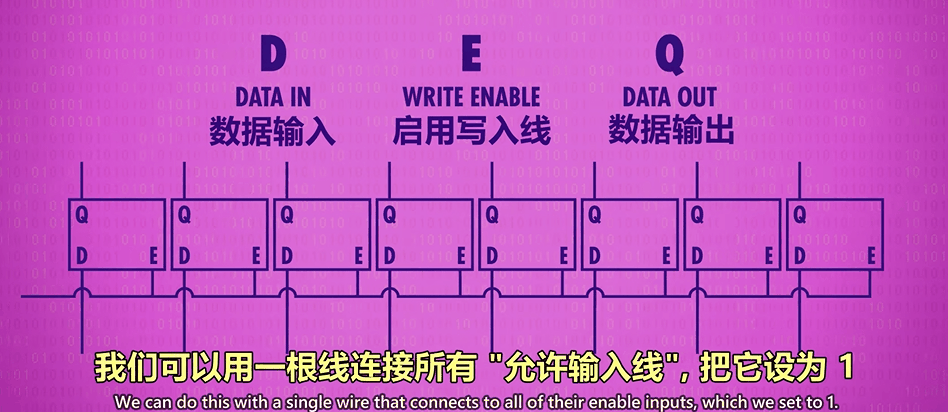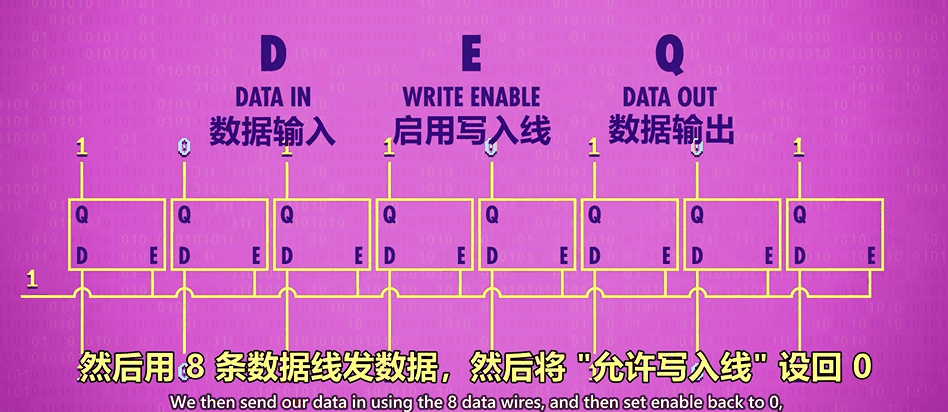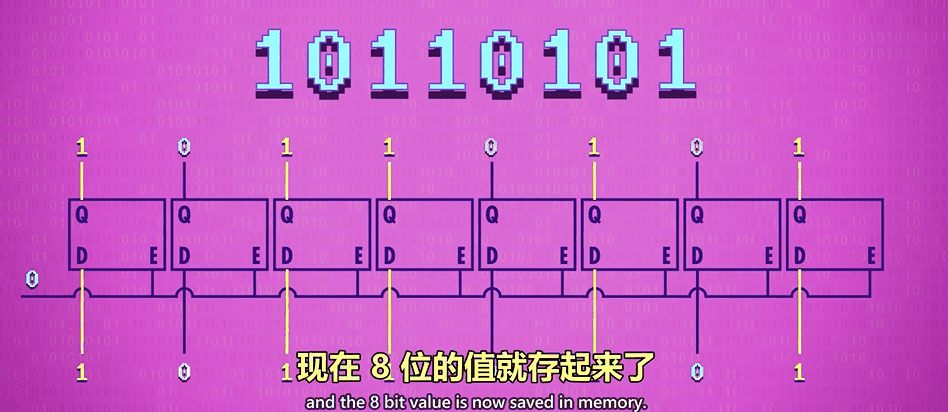
然而,这种方式,位宽越大,成本越高。因为需要的引脚翻倍增长。
- 8 位引脚数:1(允许写入)+ 8(数据输入)+ 8(数据输出)= 17
- 16 位引脚数:1(允许写入)+ 16(数据输入)+ 16(数据输出)= 33
- 32 位引脚数:1(允许写入)+ 32(数据输入)+ 32(数据输出)= 65
- 64 位引脚数:1(允许写入)+ 64(数据输入)+ 64(数据输出)= 129
- 128 位引脚数:1(允许写入)+ 129(数据输入)+ 128(数据输出)= 257
- 256 位引脚数:1(允许写入)+ 256(数据输入)+ 256(数据输出)= 513
现代计算机大多都有 64 位,这样的成本不可接受。
矩阵排列
将锁存器或触发器呈矩阵排列可以解决上述问题。
小结
知识点
- 时钟
- 锁存器
- AND-OR 锁存器
- D 锁存器
- 边沿触发
- 触发器
- SR 触发器
- D 触发器
- JK 触发器
- 存储器
参考资料
思考题答案(仅供参考)
协议
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。